为了保证机械的正常使用，对于机械中一般转速的滚动轴承应根据其当量动载荷进行寿命计算。而滚动轴承的当量动载荷指当轴承内部承受径向载荷和轴向载荷共同作用。为了与基本额定动载荷作比较，而引入的一个由实际载荷转化而成的等效载荷。

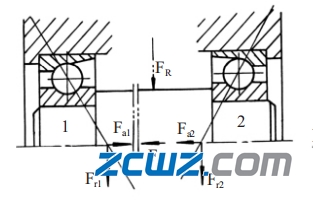
角接触轴承通常是成对使用的，根据其安装方式，可分为外圈窄边相对的正装（图 1）与外圈宽边相对的反装（图 2）。正装时轴的实际支点偏向两支点里侧；反装时轴的实际支点偏向两支点外侧。

图1 正装

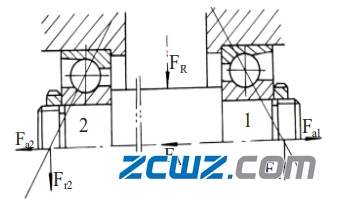
图2 反装

1、单个角接触轴承的受载分析

安装了 3 类或 7 类角接触轴承的轴，可受轴向外载荷与较大轴向外载荷的共同作用。但应注意，不管轴向外载荷的方向如何，轴承外圈对轴的轴向支反力为单向载荷，其方向由轴承外圈的宽边指向窄边。为使轴向力达到平衡，角接触轴承经常成对使用，对称安装。

当轴承内圈在轴心处受由外圈的窄边指向宽边方向的轴向外载荷 F_X 作用，且在外圈支反力作用下处于平衡时，轴承被压紧，轴承中各滚动体所承受的载荷大小相等，方向均为接触点处的法线方向，各滚动体所受支反力合力的作用点位于轴心，与且与 F_X 大小相等，方向相反。当轴承内圈在轴心处受由外圈的宽边指向窄边方向的轴向外载荷 F_X 作用时，轴承被放松，各滚动体不受轴向力的作用。故根据轴承的压紧与放松状态即可判断出其是否受轴向外载荷的作用。

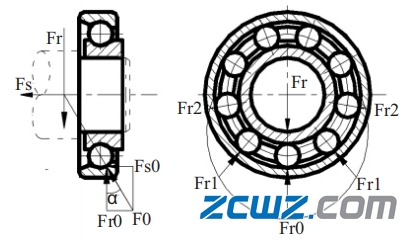
当角接触轴承受径向外载荷 F_r 作用且在外圈支反力作用下处于平衡时（图 3），内圈沿 F_r 方向下移一段距离，故上半圈滚动体不承载，而下半圈各滚动体承受不同的载荷。处 于 F_r 作用线最下位置的滚动体承载最大，而远离作用线的各滚动体承载逐渐减小。

图3 角接触轴承中径向载荷所产生的轴向分力

由于角接触轴承公称接触角 0°<α≤45°，当内圈承受纯径向载荷 F_r 时，由于 α 的存在，外圈作用在承载区第 i 个滚动体上的反力 F_i 并不指向轴承内外圈的半径方向，而是沿接触点的法线方向，它可以分解为一个径向分力F_ri 和一个轴向分力 F_si。承载区各滚动体上所受轴向分力总和即为轴承的内部轴向力 F_s，方向由轴承外圈的宽边指向其窄边。F_s 的方向与轴承内圈受纯轴向载荷被压紧时，外圈所能产生的支反力方向相同。

综合分析可知，单个轴承在轴向载荷 F_X 与径向载荷 F_r共同作用时，轴承外圈所能产生的轴向支反力 F_a 必定不会小于其只受纯径向载荷 F_r 时的内部轴向力 F_s，即为所求的变形协调条件：F_a≥F_s

2、轴承组合中角接触轴承的受载分析

在轴承组合中求轴承所受的轴向载荷，可首先求得内部轴向力，然后根据内部轴向力与外载荷判断各轴承受载的特点，分析其是受轴向载荷与径向载荷共同作用，还是只受纯径向载荷的作用，然后即可根据式(1)与式(2)求得轴向载荷。

以图 1 为例，进行分析。该图轴系结构可简化画为图 4。

图 4 正装轴承的受力分析简图

首先求得轴承的内部轴向力分别为 F_s1 与 F_s2。比较 F_s1与 F_s2+F_A 的关系，可能有以下三种情况：

（1）F_s1>F_s2+F_A，此时轴在轴向外载荷与内部轴向力作用下处于不平衡状态，轴有向右移动的趋势，右轴承 2 被压紧，左轴承 1 被放松。故轴承 1 只受纯径向载荷的作用，其轴向载荷为 F_a1=F_s1；而轴承 2 受到了径向载荷与轴向载荷的共同作用，其轴向载荷 F_a2>F_s2，再结合式（1）可得：F_a2=F_A-F_a1。

（2）F_s1=F_s2+F_A，此时轴在轴向外载荷与内部轴向力作用下达到了平衡状态，轴不会产生轴向移动，二轴承均处于放松状态，只受纯径向载荷的作用，故 F_a1=F_s1，F_a2=F_s2。

（3）Fs1<Fs2+FA，此时轴在轴向外载荷与内部轴向力作用下处于不平衡状态，轴有向左移动的趋势，左轴承1被压紧，右轴承 2 被放松。故轴承2只受纯径向载荷的作用，其轴向载荷为 F_a2=F_s2；而轴承 1 受到了径向载荷与轴向载荷的共同作用，其轴向载荷 F_a1>F_s1，再结合式（1）可得：F_a1=F_A+F_a2。

运用上述方法对图 1 进行分析，所得出的结论与教材一致。对图 2 进行分析，也可得出相同与教材相同结果；该方法对于圆锥滚子轴承轴向载荷的计算同样有效。